
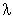 ).
If the rate of mutation (structural change) is small, intermediate
can be treated as constant during the taking of individual data
points, i.e., the material is considered 'quasi-stable'.
).
If the rate of mutation (structural change) is small, intermediate
can be treated as constant during the taking of individual data
points, i.e., the material is considered 'quasi-stable'.

| Figure 1: storage modulus G' and loss modulus G" for a sample which crosslinks with increasing reaction time. Curves are shown for three frequencies. The instant at gelation is marked with a vertical line (at about t=1200 s). For a more complete characterization of the material, data is also needed at different frequencies. |
 t. Steady conditions in a
dynamic mechanical experiment are reached after about one period
t. Steady conditions in a
dynamic mechanical experiment are reached after about one period
 .
.
 | Figure 2: Characteristic time of dynamic mechanical experiment
 . .
|
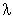 is the time constant of the relaxation mode which dominates the
rheometrical experiment. For steady conditions (steady shear
viscosity, equilbrium modulus), this is the longest relaxation time
is the time constant of the relaxation mode which dominates the
rheometrical experiment. For steady conditions (steady shear
viscosity, equilbrium modulus), this is the longest relaxation time
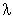 max.
In a dynamic mechanical experiment, the stress response is dominated
by relaxation processes with a time constant near
1/
max.
In a dynamic mechanical experiment, the stress response is dominated
by relaxation processes with a time constant near
1/ .
.
 | Figure 3: Fading memory of a material as described by the relaxation modulus. In this schematic, the relaxation is demonstrated by a single exponential. |
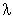 mu
is the characteristic time constant for the change in
the material. The change is measured indirectly through the property
of interest, g (e.g. G', G").
mu
is the characteristic time constant for the change in
the material. The change is measured indirectly through the property
of interest, g (e.g. G', G").
 | Figure 4: Schematic of the change of the measured property g. The mutation time is the inverse of the rate of change of property g. |



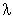 /
/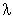 mu<<1 the
material is quasi-stable and TRR is possible
mu<<1 the
material is quasi-stable and TRR is possible
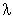 /
/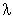 mu > 1 the
sample changes during the relaxation process and no reliable data can
be taken, e.g. a fast changing sample at low frequencies
mu > 1 the
sample changes during the relaxation process and no reliable data can
be taken, e.g. a fast changing sample at low frequencies

| Figure 5: Schematic of data (here: loss tangent) during a cyclic frequency sweep experiment. The
frequency window ( 1
- 1
-
 3) is scanned repeatedly. Each data point represents a
different state of the material.
3) is scanned repeatedly. Each data point represents a
different state of the material. |
 | Figure 6: Evolution of dynamic moduli during crosslinking at the three different frequencies 1, 10, and 100 rad/s. Open symbols: G', filled symbols: G". | |
 | Figure 7: Dynamic moduli at three different stages of crosslinking as interpolated with GELPRO. Open symbols: G', filled symbols: G". The lowest data set (squares) represents the material in the liquid state, the one in the center (diamonds) corresponds to the gel point, and the top data set (triangles) is the material in the solid state. |
The interactive computer program allows easy graphical representation of the dynamic moduli, the loss tangent, the rate of change of the dynamic moduli and several other material functions as functions of time and frequency. The mutation number can be evaluated for each data point. To ensure data reliability Nmu should be less than about 0.1.
 | Figure 8: Evolution of loss tangent during crosslinking. The gel point can be determined from the crossover (at around t=2300 s). Each curve is measured at constant frequency (1, 10, 100 rad/s) | |
 |
Figure 9: Loss angle as function of frequency at three different material states. Top curve: before gel point, middle: very near gel point, bottom: beyond gel point. |
In summary, time-resolved rheometry is a very useful experimental tool
to study the rheological behavior and the transition kinetics of any
kind of material with transient properties.
IRIS DEVELOPMENT
14 Elm Street
Amherst, MA 01002-2007
USA
e-mail: IRISrheo@yahoo.com
FAX (413) 549 4129
Return to GELPRO