Definition of Relaxation Time Spectrum and Retardation Time Spectrum

Any G', G" data file, including the master file after time-temperature superposition, may be expressed by its discrete relaxation time spectrum. IRIS expresses the relaxation modulus as a sum of N Maxwell modes

                                                                       (1),

where the coefficients, , and the relaxation times, , are material parameters.  The equilibrium modulus, , is zero for fluids and finite for solid materials.

The time-dependent part of the relaxation modulus is the Laplace transform of the relaxation time spectrum , as defined in the following

                                                        (2).

Determining the Spectra

A method of determining the coefficients, , and the relaxation times, , has been developed by Baumgärtel and Winter (Rheologica Acta, 1989 and J. Non-Newtonian Fluid Mech, 1992, 1997).  Baumgärtel’s method is based on two major premises; these are (1) the simultaneous fitting of G’ and G” in order to robust the numerical algorithm, and (2) property of the solution as shown in the Baumgärtel plot, see figure below.

 

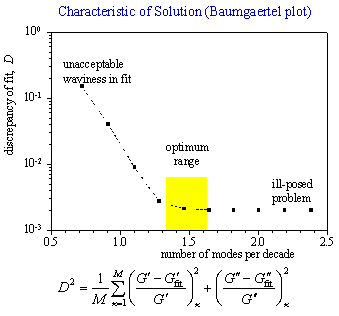
Baumgärtel realized that the admissible number of modes per decade depends on the noise in the data and, thus, can not be chosen freely. This observation was incorporated in the solution algorithm to prevent ‘overfitting’. Based on Baumgärtel’s observation, IRIS optimizes the number of modes N. However, an upper bound of N can be prescribed by the user (set value in dialog of spectrum calculation). A reduction of N , for instance, becomes necessary when using the data in computational codes (flow modeling) that is unable to accommodate a full spectrum.

The resulting discrete spectrum may be converted into discrete points of the continuous spectrum H(l).  In addition, IRIS automatically converts the discrete relaxation time spectrum into a retardation time spectrum. 

 

The following criteria have been used as guidance for developing the algorithm:

1.  Good fit of the experimental data, i.e. small standard deviation between fit and data.

2.  Avoiding of overfitting.  The algorithm has to be able to find the optimum amount of detail which can be extracted from experimental data without producing artifacts.  We suggest to keep the standard deviation of the fit (point 1 in this list) EQUAL or ABOVE the standard deviation in the data due to noise.

3.  The format of H(l) should not be predetermined.  It has to be freely adjustable during the inversion of the data.

4.  The resulting material parameters should have physical meaning.

5.  Minimization of the truncation error.  The data are always cut off on both sides of the frequency scale.  This truncation may be the source of substantial error (Jackson et al., 1992).

6.  Checking of experimental data quality.  The data are always inconsistent to some degree since the signal to noise ratios differ for G' and G".  This may cause a substantial discrepancy between fit and data which can be detected during data analysis.

7.  For practical considerations, H(l) should be expressed by a function or a sum of functions which can be integrated easily in the various linear viscoelastic model calculations. This again leads us to exponential functions for H(l).

8.  For practical considerations, the number of parameters should be small (for ease of use in modeling calculations and for storing material data in a data bank).

9.  For practical considerations, the computation time should be short.  All conversion methods in the literature seem to satisfy this criterion, due to the high computation speed of desk top computers.

We attempted to satisfy most of these conditions while keeping the algorithm as simple as possible (no curve-fitting input from user required).