Tube Dilation Theory of T. McLeish and Coworkers
The IRIS Module was written by R. Blackwell
A systematic theory has been implemented, which builds on the architecture-specific Tube-Dilation theory for linear rheology. This module was developed in collaboration with Richard Blackwell, Cambridge (UK) who implemented newer theories of Tom McLeish and his coworkers. The object of the theory module is to predict the nonlinear viscoelastic properties for monodisperse polymers, which a regular branching structure.
The models produce transient stress functions in start-up flow. Deformation is at a constant rate for a specified time, followed by relaxation.
The models are based on the tube ideas of Doi and Edwards. As for the linear rheology, a separate form of theory must be used for each molecular architecture. The architectures currently available in the module are: linear, star, pompom, and tree-like. Any of these models can be graphed by choosing ‘NLV Theory’ in the menu; continue with ‘tube dilation’ and choose from the list of molecular architectures. Parameter values are suggested and can be further chosen at that time.
Exact predictions are made for the nonlinear viscoelastic response by specifying the molecular architecture, along with a single time constant and stress modulus. Limitations are that the polymers must be monodisperse and of a regular branching structure (see the section on linear Tube-Dilation theory).
|
Figure: Molecular architecture: linear, star, pom-pom, tree |
How it works
We start with the spectrum of relaxation times calculated for the linear viscoelastic response. The branched molecular chain is separated into layers, with the outer layers relaxing faster than the inner layers. Moreover, each section of the chain between branching points relaxes on a timescale which exponentially separated from the sections of chain in the other layers of the molecule. These relaxation times are used to calculate the nonlinear dynamics of the chain.
Stress in polymer melts arises from the entropic penalty for moving the molecular chains away from an un-deformed state. After a deformation, the chains will move past each other and return to an equilibrium. In the tube model we focus on a single chain and represent the constraining effect of the other chains by a tube. To reach equilibrium our chain must escape from its tube. The stress in the melt is then given from the ensemble average over all the escaping chains.
By using the exponential separation of relaxation times in the molecule we can further focus on to a single section of chain at any given timescale. Any other sections of chain will either be moving so quickly they simply act as a solvent, or so slowly that they form a fixed polymer network.
Under a deformation we assume that the tube deforms affinely, initially taking our chain-section with it. Looking at the chain-section, we separate the deformation into a stretching component and an orientational component. The chain will relax its (average) stretch and orientation by two different mechanisms, resulting in separate relaxation times and differential equations for each.
Orientation relaxes with the first passage of the chain along the tube. This gives exactly the relaxation time used in the linear viscoelastic calculation. By contrast, the stretch can equilibrate rapidly along the tube between branch points. The stretch variable we calculate is simply the mean separation of the two ends of the section of chain. Stretch relaxation therefore occurs faster than the orientational relaxation of the innermost parts of our chain section.
|
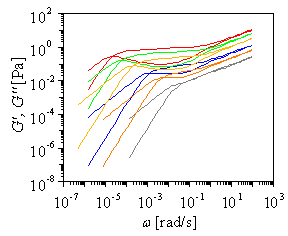
Figure: Linear chains with M/Me=60; prdiction of dynamic moduli with theory of McLeish and Milner. polymer concentration of 100, 80, 60, 40, 20% |
|
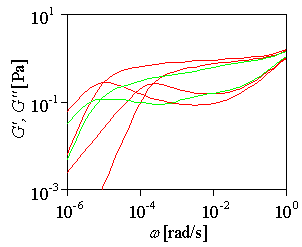
Figure: Dynamic moduli, G',G" , calculated for pom-pom polymer and, in comparison, for two linear polymers, M/Me=20 and 40. |
|
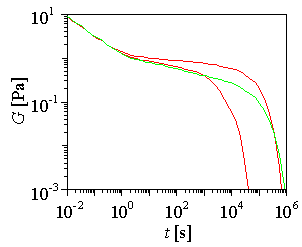
Figure: Relaxation modulus calculated for pom-pom polymer and, in comparison, for two linear polymers, M/Me=20 and 40. |
Blackwell RJ, Harlen OG, McLeish TCB (2001) Theoretical linear and nonlinear rheology of symmetric treelike polymer melts. Macromolecules 34:2579-2596
McLeish TCB, Allgaier J, Bick DK, Bishko G, Biswas P, Blackwell R, Blottiere B, Clarke N, Gibbs B, Groves DJ, Hakiki A, Hoenan RK, Johnson JM, Kant R, Read DJ, Young RN (1999) Dynamics of entangled H-polymers: teory, rheology, and neutron scattering. Macromolecules 32:6734-6758
McLeish TCB, Larson RG (1998) Molecular constitutive equations for a class of branched polymers: the pom-pom polymer. J Rheol 42: 81-110
Milner ST. McLeish TCB (1997) Parameter-free theory for stress relaxation in star polymer melts. Macromolecules 30:2159-2166
Milner ST; McLeish, TCB (1998) Reptation and contour-length fluctuations in melts of linear polymers. Phys Rev Lett 81:725-728.
Pryke A, Blackwell R J, McLeish TCB, Young RN (2002) Synthesis, hydrogenation, and rheology of 1,2-polybutadiene star polymers. Macromolecules 35:467-472