Accessing Molecular Stress Function of Manfred Wagner and coworkers
The Molecular Stress Function (MSF) theory allows modeling of the nonlinear rheology of polymer melts and concentrated solutions by use of one (linear polymers, extension), two (linear polymers, shear; branched polymers, extension), or three (branched polymers, shear) model parameters. In the model, a chain segment is defined as an entropic entity which, in the linear-viscoelastic limit, gives rise to one entanglement contribution to the plateau modulus. According to the model, chain segments of branched polymers fall into two distinct categories: either they belong to the backbone of the macromolecule and are stretched by nonlinear deformation, or they do not belong to the backbone (i.e. are oriented “perpendicular” to the backbone) and are compressed by nonlinear deformation. Although this is a very simple and coarse-grained model of the complex structure of polydisperse and randomly branched polymer systems, it seems to capture the essential nonlinear parameters responsible for extensional strain-hardening and shear thinning.
|
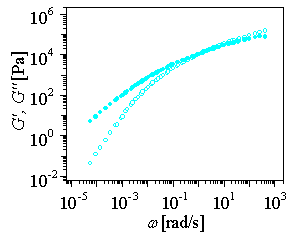
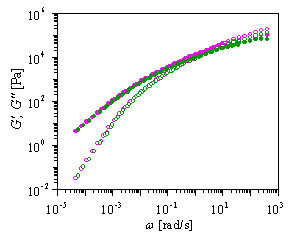
Figure: G',G" data of LLDPE at 130C |
|
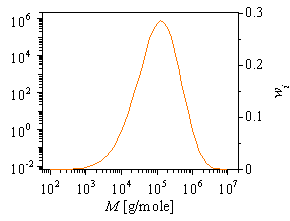
Figure: Molecular weight distribution of LLDPE sample, determined from G',G" data using the theory of Cocchini and Nobile (within IRIS) |
|
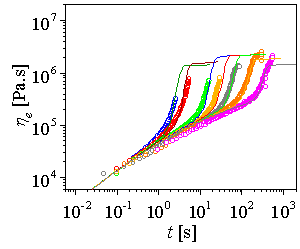
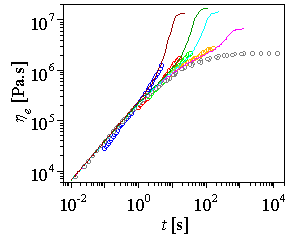
Figure: Predictions with Molecular Stress Function (MSF) theory: Comparison of uniaxial extension data of LLDPE at 130C with theoretical prediction |
Note that the simulation requires a relaxation time spectrum of your specific sample. For this reason, linear data analysis needs to precede this simulation to create a DMGJ file. This file must be highlighted in the ‘Project Explorer and Material Function’ in order to have access to the Molecular Stress Function module in NLV Theory\Melts and Solutions. After having calculated MSF-predictions (they apper in the IRIS plot), the spectrum can be deactivated in the dialog so that the newly calculated resut appears by itself. For beauty, click on ‘autoscale’ to adjust the plot.
|
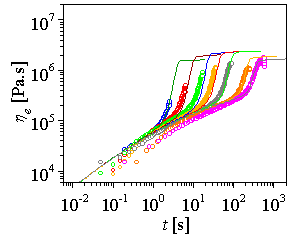
Figure: Predictions with Molecular Stress Function (MSF) theory: Comparison of uniaxial extension data of blend or 80%LLDPE and 20%HDPE (at 130C) with theoretical prediction |
|
Figure: G',G" data of LLDPE compared with G',G" data of blend or 80%LLDPE and 20%HDPE, at 130C |
|
Figure: Predictions with Molecular Stress Function (MSF) theory: Comparison of uniaxial extension data of polytyrene melt with theoretical prediction |
|
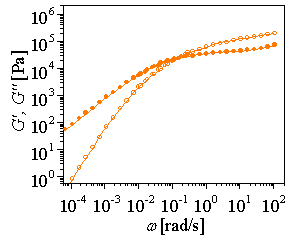
Figure: G',G" data of above polystyrene |
References
Wagner MH, Yamaguchi M, Takahashi M (2003) Quantitative assessment of strain hardening of low-density polyethylene melts by the molecular stress function model. J Rheol 47:779-793
Information about IRIS: Send your questions and suggestions to H. H. Winter at IRISrheo@.yahoo.com
back to IRIS platform